Research into black holes has taken a significant leap forward with new insights into their vibrations, known as Quasinormal Modes (QNMs). These modes represent the distinct oscillations that occur when black holes are perturbed, resembling the sound of a bell. A recent study led by Taiga Miyachi from Kyoto University introduces a novel method for analyzing these vibrations, enhancing our understanding of gravitational wave astronomy and the intricate nature of black holes.
Understanding how black holes respond to perturbations is crucial for scientists. When black holes merge, their QNMs emit vibrations powerful enough to be detected from Earth. These vibrations offer valuable data regarding the mass and shape of the black holes involved. Traditionally, measuring black hole masses has proven difficult, often relying on the orbital dynamics of surrounding stars. The new research published in Physical Review D suggests that QNMs hold fundamental information about black holes, depending solely on their mass, charge, and angular momentum, independent of their formation history.
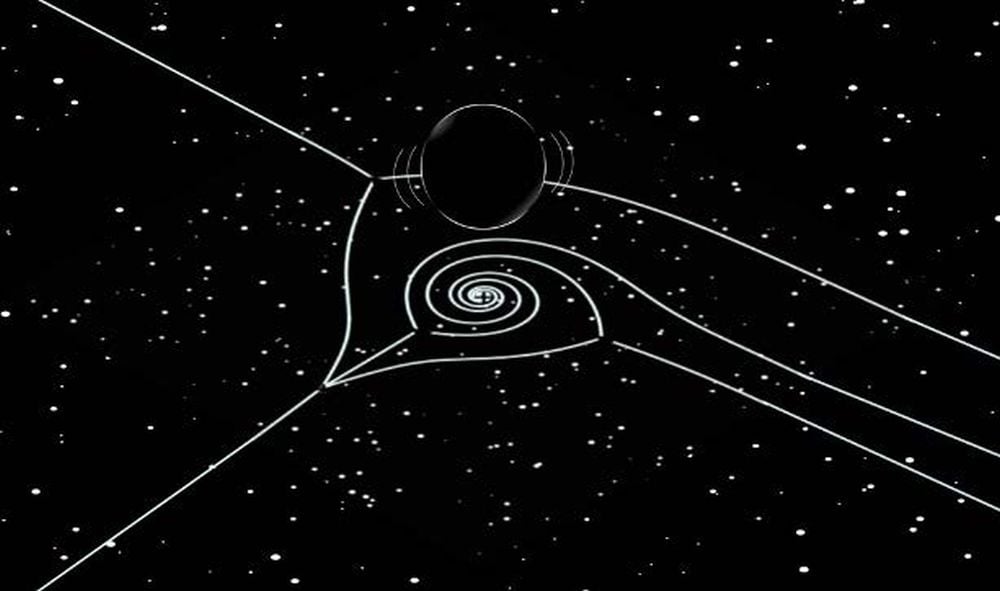
Researchers like Miyachi have focused on the complexity of QNMs, which can be defined by both real and imaginary components. The real part indicates the frequency of oscillations, while the imaginary part represents the decay rate. Their recent work emphasizes a new approach called the Wentzel–Kramers–Brillouin (WKB) method, which aims to provide a more precise analysis of these vibrations.
New Approaches to Understanding Black Holes
The team has made strides by utilizing Stokes curves in their analysis, which help mark sudden changes in wave patterns. These curves, previously overlooked in black hole studies, have revealed intricate details about the structure of black hole vibrations. “We were surprised at how complex and beautiful the underlying structure of these vibrations turned out to be,” said Miyachi. He noted that their findings include spiraling patterns that are essential for comprehending QNMs more fully.
In their conclusion, the authors assert, “the exact WKB analysis is a versatile and powerful tool for addressing black hole perturbation theories across a wide range of contexts.” This innovative approach not only furthers mathematical applications in physics but also aligns with the historical views of scientists like Galileo Galilei, who emphasized the significance of mathematics in understanding the natural world.
The potential applications of this research are substantial. With the enhanced ability to analyze black hole vibrations, astrophysicists can improve the accuracy of gravitational wave observatories. This advancement promises to deepen our understanding of black holes, offering a clearer picture of these enigmatic celestial bodies.
As research continues, the implications for gravitational wave astronomy and our grasp of the universe’s mysteries grow. The study highlights the critical intersection of mathematics and physics, paving the way for future discoveries in black hole research and beyond.







